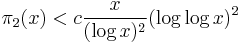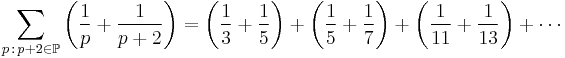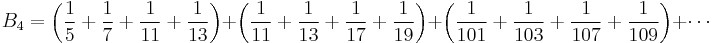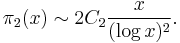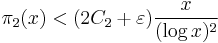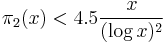Brun's theorem

In number theory, Brun's theorem was proved by Viggo Brun in 1919. It states that the sum of the reciprocals of the twin primes (pairs of prime numbers which differ by 2) is convergent with a finite value known as Brun's constant, usually denoted by B2 (sequence A065421 in OEIS). It has historical importance in the introduction of sieve methods.

Let 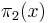\pi_2(x) denote the number of primes p ≤ x for which p + 2 is also prime (i.e. 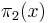\pi_2(x) is the number of twin primes with the smaller at most x). Then, for x ≥ 3, we have

\pi_2(x) < c \frac {x}{(\log x)^2} (\log\log x)^2

for some positive constant c.

This result shows that the sum of the reciprocals of the twin primes converges; in other words the p involved are a small set. In explicit terms the sum

\sum\limits_{ p \,�: \, p %2B 2 \in \mathbb{P} } {\left( {\frac{1}{p} %2B \frac{1}{{p %2B 2}}} \right)} = \left( {\frac{1}{3} %2B \frac{1}{5}} \right) %2B \left( {\frac{1}{5} %2B \frac{1}{7}} \right) %2B \left( {\frac{1}{{11}} %2B \frac{1}{{13}}} \right) %2B \cdots

either has finitely many terms or has infinitely many terms but is convergent: its value is known as Brun's constant. Unlike the case for all prime numbers, we cannot conclude from this result that there is an infinite number of twin primes.

Contents

Brun's constant

By calculating the twin primes up to 1014 (and discovering the Pentium FDIV bug along the way), Thomas R. Nicely heuristically estimated Brun's constant to be 1.902160578.[1] Nicely has extended his computation to 1.6×1015 as of 18 January 2010 but this is not the largest computation of its type.

In 2002 Pascal Sebah and Patrick Demichel used all twin primes up to 1016 to give the estimate:

B2 ≈ 1.902160583104.

It is based on extrapolation from the sum 1.830484424658... for the twin primes below 1016. Richard Crandall and Carl Pomerance reported that it is known rigorously that 1.83 < B2 < 2.347.[2] Dominic Klyve showed conditionally that B2 < 2.1754 (assuming the extended Riemann hypothesis).[3]

The digits of Brun's constant was used in a bid of $1,902,160,540 in the Nortel patent auction. The bid was posted by Google and was one of three Google bids based on mathematical constants.[4]

There is also a Brun's constant for prime quadruplets. A prime quadruplet is a pair of two twin prime pairs, separated by a distance of 4 (the smallest possible distance). The first prime quadruplets are (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109). Brun's constant for prime quadruplets, denoted by B4, is the sum of the reciprocals of all prime quadruplets:

B_4 = \left(\frac{1}{5} %2B \frac{1}{7} %2B \frac{1}{11} %2B \frac{1}{13}\right) %2B \left(\frac{1}{11} %2B \frac{1}{13} %2B \frac{1}{17} %2B \frac{1}{19}\right) %2B \left(\frac{1}{101} %2B \frac{1}{103} %2B \frac{1}{107} %2B \frac{1}{109}\right) %2B \cdots

with value:

B4 = 0.87058 83800 ± 0.00000 00005, the error range having a 99% confidence level according to Nicely.[5]

This constant should not be confused with the Brun's constant for cousin primes, prime pairs of the form (p, p + 4), which is also written as B4. Wolf derived an estimate for the Brun-type sums Bn of 4/n.

Further results

Let 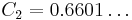C_2=0.6601\ldots (sequence A005597 in OEIS). Then it is conjectured that

\pi_2(x)\sim2C_2\frac{x}{(\log x)^2}.

In particular,

\pi_2(x)<(2C_2%2B\varepsilon)\frac{x}{(\log x)^2}

for every 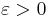\varepsilon>0 and all sufficiently large x.

Many special cases of the above have been proved. Most recently, Jie Wu proved that for sufficiently large x,

\pi_2(x) < 4.5 \frac {x}{(\log x)^2}

where 4.5 corresponds to 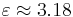\varepsilon\approx3.18 in the above.

See also

References

  1. ^ Nicely, Thomas R. (18 January 2010). "Enumeration to 1.6*10^15 of the twin primes and Brun's constant". Some Results of Computational Research in Prime Numbers (Computational Number Theory). http://www.trnicely.net/twins/twins2.html. Retrieved 16 February 2010. 
  2. ^ Crandall, Richard; Pomerance, Carl (2005). Prime Numbers: A Computational Perspective. Springer. ISBN 0387252827. 
  3. ^ Klyve, Dominic. "Explicit bounds on twin primes and Brun's Constant". http://gradworks.umi.com/33/34/3334102.html. Retrieved 31 December 2010. 
  4. ^ Damouni, Nadia (1 July 2011). "Dealtalk: Google bid "pi" for Nortel patents and lost". Reuters. http://www.reuters.com/article/2011/07/02/us-dealtalk-nortel-google-idUSTRE76104L20110702. Retrieved 6 July 2011. 
  5. ^ Nicely, Thomas R. (26 August 2008). "Enumeration to 1.6×1015 of the prime quadruplets". Some Results of Computational Research in Prime Numbers (Computational Number Theory). http://www.trnicely.net/quads/quads.html. Retrieved 9 March 2009. 

External links